The Sweet and Not So Sweet Sound of Music

Ever since monks began experimenting with complex harmony in the 11th century, people have responded differently to different intervals. Although no official documentation exists, the first interval other than the unison must have been the octave. In just temperament, an outgrowth of Pythagorean music theory, the frequency ratio between the two notes of an octave is exactly 2-to-1. As they experimented beyond the octave, musicians of all types, not just monks, discovered dissonances, which they avoided. In today’s equal temperament music world, major and minor thirds are among the most consonant of all intervals. During the 11th century, however, thirds were taboo because they were extremely dissonant in the chords of that time. This is because of just temperament’s relationship with, which based its structure on a series of perfect fifths. The circle of pure perfect fifths, however, does not end where it started. This creates a painful dissonance at the end of the series called the wolf fifth, which bridges the frequency gap. Because of this wolf fifth, keys requiring any more than three sharps or flats became so dissonant as to be impractical.

At the end of the 16th century, Galileo Galilei’s father, Vincenzo, wrote several pieces making use of equal temperament. This system, rather than using a series of pure fifths, divided the octave into 12 equal parts. Despite small changes in pure intervals, the relationship between the 12 semitones ensured greater flexibility in enharmonic expression. Instead of just a few, all 24 major and minor keys were now available because the dissonances in the interior intervals were so much smaller.

Our modern ears are now used to equal temperament, and, despite the impurities in its intervals, now prefer its sound over any other temperament. Researchers at the University of Minnesota wanted to delve more into this and studied 250 students at the University. Their main thesis question was: what makes certain combinations of notes pleasant or unpleasant?

They found that what caused an interval to be dissonant was the prevalence of “beating intervals.” Beating happens when two notes are extremely close in frequency but not exactly the same. For example, middle-C has a frequency of 512 hertz (cycles per second). Two instruments playing middle-C in unison would have no beating if both instruments produced a frequency of exactly 512 hertz. Beating would begin if one player played 512 hertz and the other played 511 or 513 hertz. Obviously, greater differences in the number of hertz would create larger beats. Larger beats would create, in turn, more and more dissonant and unpleasant sounds.

A fascinating but unexpected conclusion was that the amount of musical training in the test subjects affected the results. Subjects with more musical training than their counterparts preferred the most pleasant sounds. In other words, they preferred sounds with little or no beating. It makes sense that subjects with perfect pitch would prefer these tones, but it was apparent in those with only decent relative pitch, as well. This is indicative of how influential intonation is in musical performance, regardless of the performer’s level of training.

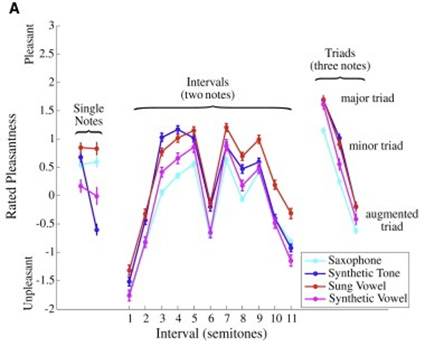
The researchers noted something else intriguing, as well. The preference for fully consonant sounds in subjects trained in Western music is absent in subjects that came from other cultures. Indeed, other tuning systems, such as that of an Indonesian Gamelan, use intervals and harmonies that would be very dissonant to a Western music ear. In fact, the tuning of many Gamelan ensembles is actually designed to create beats and dissonance. The researchers discovered that preference of consonance or dissonance varied from culture to culture.

Article in New York Times

The report

 Loading ...